Math and Measurement

Calculations in science are most often done with quantities and not simply with numbers. A quantity has a magnitude which describes the size of its value, but perhaps more importantly it has a unit which describes what the quantity measures.
When doing mathematics using quantities there are special rules concerning how to work with the units of the measurements.
The most common type of calculations found in a physics class involve multiplication and division. The rules for these calculations are the most straight forward and will be considered first.
More care has to be taken when subtracting or adding quantities. The rules for subtraction and addition will be considered second.
When doing mathematics using quantities there are special rules concerning how to work with the units of the measurements.
The most common type of calculations found in a physics class involve multiplication and division. The rules for these calculations are the most straight forward and will be considered first.
More care has to be taken when subtracting or adding quantities. The rules for subtraction and addition will be considered second.
Multiplication and Division
When multiplying or dividing quantities keep the following rules in mind:
Derived units are created because of these rules.
- Quantities with different units can be multiplied or divided
- Convert same units with different metric prefixes to the same prefix
- Same units on top and bottom of a fraction can be canceled out provided they have the same metric prefix
Examine how units are handled in the following examples.
Example 1: While on vacation, Sally drives to a campground. The trip takes 3.5 hours and the distance traveled is 308 km. What was Sally's average speed in kph (km/h)?
[Ex 1]
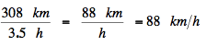
The speed 88 km/h is about the same value as 55 mph (55 mi/hr).
Example 2: The speed of light in vacuum is 3.0 x 108 m/s. How far is the nearest neighboring star, Proxima Alpha, if it takes 1.3 x 108 seconds for light to travel there?
Example 2: The speed of light in vacuum is 3.0 x 108 m/s. How far is the nearest neighboring star, Proxima Alpha, if it takes 1.3 x 108 seconds for light to travel there?
[Ex 2]
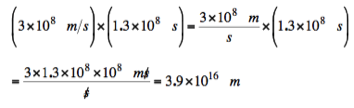
Example 3: What is the average speed (km/h) of the planet Mars if it takes 1.8 x 104 h to travel the 1300 million kilometers around the Sun?
[Ex 3]
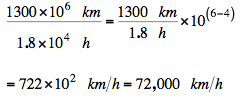
Addition and Subtraction
When adding or subtracting quantities keep the following rules in mind:
- Only add or subtract the same kind of quantities which have the same units
- Only add or subtract quantities with the same power of 10
- Only add or subtract quantities with the same metric prefix
An example of Rule (1) note that it is impossible to add twelve kilograms of mass to twenty newtons of force:
[Ex 4]
12 kg + 20 N = CAN NOT BE DONE
Mass (kg) and force (N) can not be added together because they are different kinds of quantities.
Rules (2) and (3) really express the same idea since a metric prefix is just another way of writing a power of ten.
Consider the following example:
Rules (2) and (3) really express the same idea since a metric prefix is just another way of writing a power of ten.
Consider the following example:
[Ex 5]
(3 km) - (0.2 x 103 dam) = ?
Both dekameters (dam) and kilometers (km) measure the same kind of quantity, length. As a first step, convert both numbers to the same metric prefix. The next section will explain how to convert one unit into another. But you can always convert to the base unit (in this case, meters) by replacing the metric prefix with the corresponding power of ten:
[Ex 5a]
= (3 x 103 m) - (0.2 x 103 x 101 m)
The second term can be simplified by combining the two powers of ten:
[Ex 5b]
= (3 x 103 m) - (0.2 x 104 m)
It is possible at this step to enter the numbers into a calculator because both numbers have the same unit. But let's complete the calculation by hand. It is necessary to get both numbers to have the same power of ten. This can be done by noting that 3 = 0.3 x 101:
[Ex 5c]
= (0.3 x 101 x 103 m) - (0.2 x 104 m)
[Ex 5d]
= (0.3 x 104 m) - (0.2 x 104 m)
[Ex 5e]
= (0.3 -0.2) x 104 m = 0.1 x 104 m
Although there is nothing wrong with the answer as written, note that
[Ex 5f]
0.1 x 104 m = 1 x 103 m = 1 km

What is
3.0 x 102 A + 2.2 x 104 mA?
(click for answer)
