Math and Measurement

Significant Figures
Every measurement has a precision determined by the design of the tool used to make the measurement. A measurement is written to communicate the precision of the measurement to the reader. For example
• the length of the pencil is 12 cm (two significant figures)
• the length of the pencil is 12.5 cm (three significant figures)
• the length of the pencil is 12.4671 cm (six significant figures)
• the length of the pencil is 12.5 cm (three significant figures)
• the length of the pencil is 12.4671 cm (six significant figures)
It is very important not to imply that a measurement is more precise than the measurement actually made. The number of digits used to record the measurement represent the precision of the measurement. The digits are referred as significant figures.
Any non-zero number in a measurement is a significant figure.
The only number in a measurement which may not be significant is a zero. Often a zero is written as a placeholder for a power of ten and is not part of the measurement.
• 1000 m - three zeros represent the tens, hundreds, and thousands place
• 0.05 m - zeros are used to indicate the hundredths place
• 0.05 m - zeros are used to indicate the hundredths place
The following rules will help in deciding whether a zero is significant:
Rules for Determining when a "0" is Significant:
1) Any zero between non-zero digits is significant | a. 103 m has three significant figures b. 0.01002 s has four significant figures (the first two zeros are place holders) | a | 10-1 | deci- | d |
2) Zeros written at the beginning of a number are NOT significant (they are placeholder zeros) | a. 0.0013 kg has two significant figures b. 0.102 m has three significant figures | a | 10-1 | deci- | d |
3) Zeros written at the end of a number after a decimal point ARE significant | a. 13.200 g has five significant figures. Note that the zeros at the end are not needed OTHER than to indicate precision (13.2 g is the same size as 13.200 g) b. 3500 m has two significant figures (the last two zeros are not after a decimal point, they are being used as place holders) | a | 10-1 | deci- | d |
4) Zeros at the end of a number without a decimal point MAY be significant if the "0" is part of the measurement. Confusion should be avoided by using scientific notation | a. 1000 m could have one, two, three, or four significant figures Use scientific notation to specify the number of significant digits in the measurement 1.000 x 103 m (four significant figures) 1.00 x 103 m (three significant figures) 1.0 x 103 m (two significant figures) 1 x 103 m (one significant figure) | a | 10-1 | deci- | d |

How many significant figures in
a) 450 m
b) 3.20 x 105 g
c) 0.00340 mL
(click for answer)

a) two
b) three
c) three
Using Significant Figures in Calculations
When doing mathematics with measurements the result should not imply a greater precision than the measurements used in the calculation.
Multiplying and Dividing with Significant Figures
There are two rules for doing calculations, one for multiplication and division and another for addition and subtraction (much like doing calculations with SI prefixes)
When multiplying or dividing measured quantities the final answer should be rounded to the LEAST number of significant figures used in the calculation.
Example 1: What is area of a rectangular plot of land that measure 5.32 m on one side and 4.0 m on the other?
Strategy: The area of a rectangle is length x width. The smallest number of significant figures used in the problem is two (4.0 m has two significant figures), so the final answer should be rounded to two significant figures
Strategy: The area of a rectangle is length x width. The smallest number of significant figures used in the problem is two (4.0 m has two significant figures), so the final answer should be rounded to two significant figures
Area = Length x Width
= 5.32 m x 4.0 m
= 21.28 m
= 21 m (two significant figures)
= 5.32 m x 4.0 m
= 21.28 m
= 21 m (two significant figures)
Example 2: What is the density of a stone that has a volume of 15.2 mL and a mass of 120.2 g?
Strategy: The density of an object is defined to be mass / volume. The smallest number of significant figures in the problem is three (15.2 mL has three significant figures)
Strategy: The density of an object is defined to be mass / volume. The smallest number of significant figures in the problem is three (15.2 mL has three significant figures)
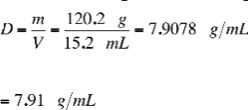
Adding and Subtracting with Significant Figures
Unfortunately simply rounding the answer to the least number of significant figures is NOT a useful approach when adding or subtracting. To understand why, consider the following example,
Example 3: What is the perimeter of a triangle which has sides equal to 11 cm, 2.15 cm, and 0.8 cm?
Strategy: The perimeter of the triangle is equal to the sum of its sides. The smallest number of significant figures in the problem is one (0.8 cm)
P = 11 cm + 2.15 cm + 0.8 cm
= 13.95 cm
= 10 cm (one significant figure)
THIS IS INCORRECT!
= 13.95 cm
= 10 cm (one significant figure)
THIS IS INCORRECT!
The problem with the solution shown above is that by rounding to one significant figure the precision of the answer is only within 10 cm, but the least precise measurement was to within a centimeter (11 cm implies that the measurement was estimated to the nearest centimeter). When adding or subtracting measurements rounding to the lowest number of significant figures will result in an answer with too little precision!
So what is the correct method for adding and subtracting measurements?
So what is the correct method for adding and subtracting measurements?
When adding or subtracting measured quantities the final answer should be rounded to the same precision as the LEAST PRECISE value used in the calculation.
Let's take another look at Example 3:
Example 3: What is the perimeter of a triangle which has sides equal to 11.2 cm, 2.15 cm, and 4 cm?
Strategy: The perimeter of the triangle is equal to the sum of its sides. The LEAST PRECISE value is 11 cm which indicates the answer should be rounded to the nearest centimeter.
Example 3: What is the perimeter of a triangle which has sides equal to 11.2 cm, 2.15 cm, and 4 cm?
Strategy: The perimeter of the triangle is equal to the sum of its sides. The LEAST PRECISE value is 11 cm which indicates the answer should be rounded to the nearest centimeter.
P = 11 cm + 2.15 cm + 0.8 cm
= 13.95 cm
= 14 cm (rounded to closest 1 cm)
CORRECT!
= 13.95 cm
= 14 cm (rounded to closest 1 cm)
CORRECT!
As a practical matter, adding or subtracting measurements of different precision does not occur too often in physics class. In most cases the measurements in an experiment will be done using the same tool (meter stick, graduate cylinder, scale, etc.). Measurements made with the same tool should have the same precision.

(A) 42 cm x 50 cm = ?
(B) 435 g / 32 mL = ?
(C) 230 g + 6 g = ?
(D) 1200 m - 23.3 m = ?
(click for answer)

(A) 42 cm x 50 cm = 2000 cm2
(B) 435 g / 32 mL = 14 g/mL
(C) 230 g + 6 g = 240 g
(D) 1200 m - 23.3 m = 1200 m
A Final Note on Rounding Measurements...
Most of the time it is obvious how to round the result of a calculation to the correct number significant figures. But care should be taken if the last non-zero digit in a number is "5".
In each of the following examples, a measurement will be rounded to three significant figures.
Rules for Rounding in Calculations
Whenever the last significant figure is followed by a 0, 1, 2, 3, or 4 ROUND THE RESULT DOWN | 12.42 cm would round to 12.4 cm |
Whenever the last significant figure is followed by a 6, 7, 8, or 9 ROUND THE RESULT UP | 12.46 cm would round to 12.5 cm |
The following rules apply ONLY if the last significant digit is followed by a "5"
If the last significant figure is followed by a "5" with additional nonzero digits ROUND THE RESULT UP | 12.4502 cm would round to 12.5 cm |
If the last significant figure is an EVEN digit followed by a "5" with NO additional nonzero digits ROUND THE RESULT DOWN | 12.4500 cm would round to 12.4 cm |
If the last significant figure is an ODD digit followed by a "5" with NO additional nonzero digits ROUND THE RESULT UP | 12.5500 cm would round to 12.6 cm |
The rounding rules for numbers ending in "5" may seem strange, but the purpose is to insure that results are not always rounded upwards creating a systematic error.
Remember! The only time there is a special rule for rounding a number is if the first NONSIGNIFICANT DIGIT IS EXACTLY "5".
Generally, that specific case does not happen too often.
Remember! The only time there is a special rule for rounding a number is if the first NONSIGNIFICANT DIGIT IS EXACTLY "5".
Generally, that specific case does not happen too often.