Math and Measurement

Science uses mathematics to understand the relationship between quantities, unlike a simple number a quantity represents something that can be measured in the physical world.
SI units identify the type of quantity, for example meters are used for "length" and kilograms are used for "mass". A prefix helps to specify the size of the measured quantity, one kilogram (kg) is 100 times larger than one dekagram (dag).
Measurements are made using tools. The tools used to measure a quantity range from the very simple to the incredibly complex.
SI units identify the type of quantity, for example meters are used for "length" and kilograms are used for "mass". A prefix helps to specify the size of the measured quantity, one kilogram (kg) is 100 times larger than one dekagram (dag).
Measurements are made using tools. The tools used to measure a quantity range from the very simple to the incredibly complex.
Length can be measured very simply using a meter stick, which is often just a marked piece of wood. A meter stick will provide a very acceptable measurement of the length of your shoe. But a meter stick is of little use to a biologist studying the anatomy of a dust mite. A different tool is needed to measure length on that scale, such as an electron microscope.

Figure 1: Electron microscope image of the common dust mite which typically measure about 0.4 mm (0.016 inch) long. Dust mites are found in every home and live by consuming flakes of skin that fall off the human body.
The quality of a measurement is described by its accuracy and precision.
Precision
Precision refers to the exactness of a measurement. The precision of a measurement depends on the tool used to make the measurement.
The image below shows a pencil being measured by three different rulers.
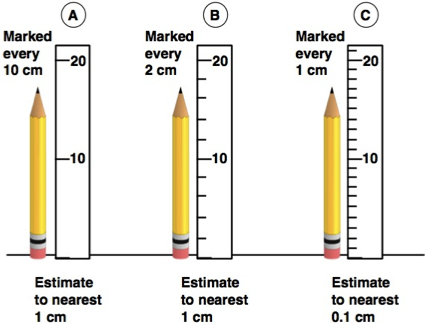
Figure 2: Three rulers of different precision.
Ruler A is only marked in 10 cm intervals and is less precise than Ruler B which is marked in 2 cm intervals. The most precise ruler is Ruler C which is marked every 1 cm.
The general rule of making a measurement with a linear scale (like the scale marked on a ruler or graduated cylinder) is to estimate one more unit than is marked on the scale.
In the figure above, each pencil is the same size, but the precision of each measurement is different
Ruler A: Pencil is about 17 cm
Ruler B: Pencil is close to 17 cm
Ruler C: Pencil is 17.2 cm
Ruler B: Pencil is close to 17 cm
Ruler C: Pencil is 17.2 cm
Note that using Ruler A or Ruler B results in a measured length of about 17 cm, but a person using Ruler B can be more confident in the measurement because Ruler B is more precise than Ruler A.
Since Ruler C is marked every 1 cm, the person making the measurement should estimate to the closest 0.1 cm. The measurement of the pencil length is 17.2 cm, where the "0.2" part of the measurement is an estimate made by the person reading the ruler. It is quite possible that another person would record the length as 17.1 cm or 17.3 cm, they are also valid measurements. It is assumed that the last digit in a measurement is only an estimate.
Since Ruler C is marked every 1 cm, the person making the measurement should estimate to the closest 0.1 cm. The measurement of the pencil length is 17.2 cm, where the "0.2" part of the measurement is an estimate made by the person reading the ruler. It is quite possible that another person would record the length as 17.1 cm or 17.3 cm, they are also valid measurements. It is assumed that the last digit in a measurement is only an estimate.
Accuracy
Accuracy describes how close a measurement is to its actual value. The accuracy of a measurement depends on the construction of the measurement tool as well as how the tool is used when making the measurement.
The accuracy of a measuring device can vary depending on its design, construction, or condition.
Consider the three rulers shown in Figure 3. The rulers do not have the same precision. It is easy to see that Ruler B is the least precise while Ruler C is most precise. But is Ruler C the BEST one to use to make a measurement?
The most precise ruler is useless if it is not accurate. But how accurate are the rulers? Accuracy is best determined by comparing each ruler to a known standard, such as another ruler which is KNOWN to be accurate.
Consider the three rulers shown in Figure 3. The rulers do not have the same precision. It is easy to see that Ruler B is the least precise while Ruler C is most precise. But is Ruler C the BEST one to use to make a measurement?
The most precise ruler is useless if it is not accurate. But how accurate are the rulers? Accuracy is best determined by comparing each ruler to a known standard, such as another ruler which is KNOWN to be accurate.
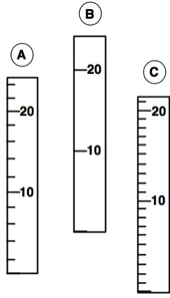
Figure 3: Three rulers of different precision.
The more precise measuring device is not the best one to choose if it is not accurate.
Figure 4 shows the same three rulers being used to measure the height of a cat.
Figure 4 shows the same three rulers being used to measure the height of a cat.
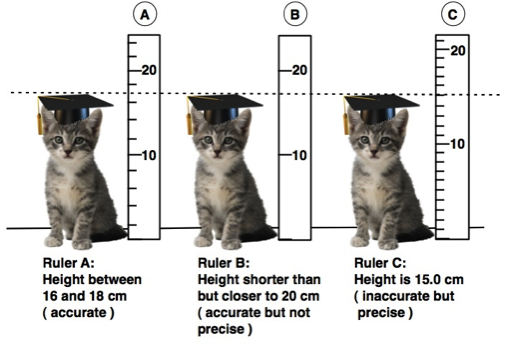
Figure 4: Ruler A and Ruler B both agree on the height of the cat. The measurement made by Ruler A is more precise than Ruler B, but they are both accurate. The measurement made by Ruler C is the most precise but it is inaccurate and Ruler C should not be used.
Although it is possible to have a ruler that is inaccurate (especially a school ruler that's been banged around for a decade or two!), it is more common to make an error while making a measurement with the ruler.
A common error when reading a ruler is caused when the eye is not directly align with the object being measured. This results in a parallax error, which leads to an inaccurate measurement.
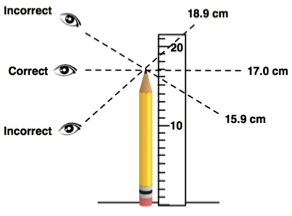
Figure 5: Reading a ruler from above or below the tip of the pencil creates an inaccurate measurement due to parallax errors
Refer to the measurement of the pencil in Figure 5. The correct measurement for the length of the pencil is 17.0 cm. An incorrect measurement will result if the ruler is read from above (15.9 cm is too small a value). Reading the ruler from below will also result in a measurement that is inaccurate (18.9 cm is too large a value).