Math and Measurement

The factor-label method is used to convert between units that measure the same kind of quantity (eg. convert a length measurement from inches to centimeters). Dimensional analysis closely resembles the factor-label method, but dimensional analysis examines the units in a calculation to help verify the calculation is correct.
Factor-Label Method
The factor-label method uses special fractions called conversion factors to change between units. The numerator and denominator are the same size and quantity:
[eq 1]
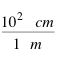
The fraction shown in [eq 1] is an example of a conversion factor. Both the top and the bottom of the fraction is the same size and quantity which makes the value of the fraction equal to 1 (note that the value IS NOT 100 because the units on the top and bottom do not cancel). The magnitude of any measurement will not be changed by multiplying by 1, so the conversion factor can be used to convert a measurement in meters to centimeters:
[eq 2]
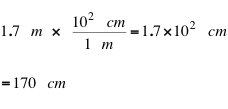
Converting from meters to centimeters is not terribly difficult and most students would probably do the conversion by inspection (a fancy way of saying in their head) . But conversion factors can also be used to convert imperial units to SI units and vice versa.
The following example uses the fact that 1 inch = 2.54 cm and that 1 feet = 12 inches. It also shows how conversion factors can be chained together:
The following example uses the fact that 1 inch = 2.54 cm and that 1 feet = 12 inches. It also shows how conversion factors can be chained together:
[eq 3]
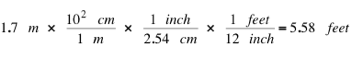
Note that 5.58 feet is about 5 foot 7 inches.
Dimensional Analysis
Dimensional analysis can be used to quickly check for errors in a calculation. For a simple calculation, dimensional analysis may actually tell you how to do the calculation!
For example, consider two students, Goofus and Gallant, asked to solve the following question involving density:
Question: A standard gold bar has a mass of about 14 500 grams. What is the volume of the gold bar? The density of gold is 19.5 g/mL.
Question: A standard gold bar has a mass of about 14 500 grams. What is the volume of the gold bar? The density of gold is 19.5 g/mL.

Goofus and Gallant from Highlights magazine
Goofus does not remember the formula to calculate density and does not use units in his calculations. Here is Goofus' INCORRECT solution:
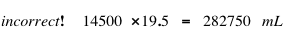
Gallant also does not remember the formula for density, but he does pay attention to units. Since the mass of gold is in grams (g), Gallant reasons that it is necessary to use the density (g/mL) to CANCEL grams in the calculation:
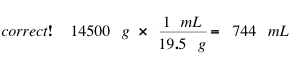
Note that the density 19.5 g/mL can be correctly expressed as (19.5 g) / (1 mL).
Gallant can also determine the formula for density from the units given in the question. Remembering that mass is measured in grams (g) and volume in milliliters (mL):
Gallant can also determine the formula for density from the units given in the question. Remembering that mass is measured in grams (g) and volume in milliliters (mL):
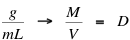
The formula for denisty is mass divided by volume ( D = M / V ).

How many seconds (s) does it take a car traveling at 25 m/s to cover a distance of 450 meters? Use dimensional analysis!
(click for answer)
